Find leaks in Delphi with Deleaker
Recently I’ve met Uwe Schuster’s tweet regarding an issue with TPngImage class.
It is not possible to have lots of TPngImage instances?
Doing so will result in a crash in FillChar in TChunkIHDR.PrepareImageData.
— Uwe Schuster (@UScLE) January 6, 2020
The test code is a simple loop that creates a TPngImage and loads it from a stream to eventually make a cache strategy decision based on the required mem. After the loop all instances are freed.
4000 times with $(BDSBIN)\iOSDelphiIcon.png works, but 5000 does lead to the AV
— Uwe Schuster (@UScLE) January 6, 2020
I’ve been curious to try to debug this. And also it was a good chance to try Deleaker. Deleaker is a tool that finds any leaks: memory, GDI, handles and others. Artem Razin, it’s author, was so kind to give me Deleaker for a honest review. And this paricular case definetely looks like some sort of leak.
First of all, I’ve reproduced the test code, as Uwe described (I’m using Delphi 10.3.3):
function LoadPngFromStream(const Stream: TStream): TPngImage;
begin
Result := TPngImage.Create;
try
Result.LoadFromStream(Stream);
except
Result.Free;
raise;
end;
end;
procedure TForm6.Button1Click(Sender: TObject);
var
Stream: TFileStream;
I: Integer;
ImageList: TObjectList<TPngImage>;
begin
Stream := TFileStream.Create('C:\Program Files (x86)\Embarcadero\Studio\20.0\bin\iOSDelphiIcon.png', fmOpenRead);
try
ImageList := TObjectList<TPngImage>.Create(True);
try
// creating 5000 instances of TPngImage
for I := 1 to 5000 do
begin
Stream.Position := 0;
ImageList.Add(LoadPngFromStream(Stream));
end;
finally
ImageList.Free;
end;
finally
Stream.Free;
end;
end;
And this is true, it fails with an exception: “Project Project3.exe raised exception class $C0000005 with message ‘access violation at 0x00407867: write of address 0x00000000′”.
Let’s check GDI handles usage with Deleaker.
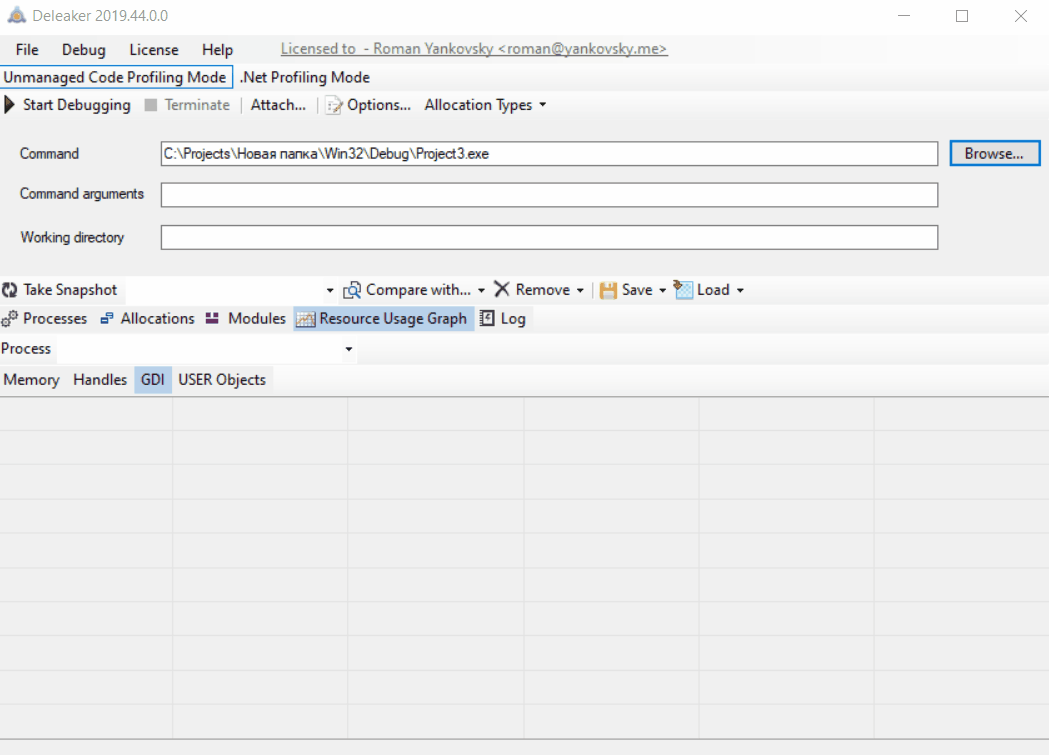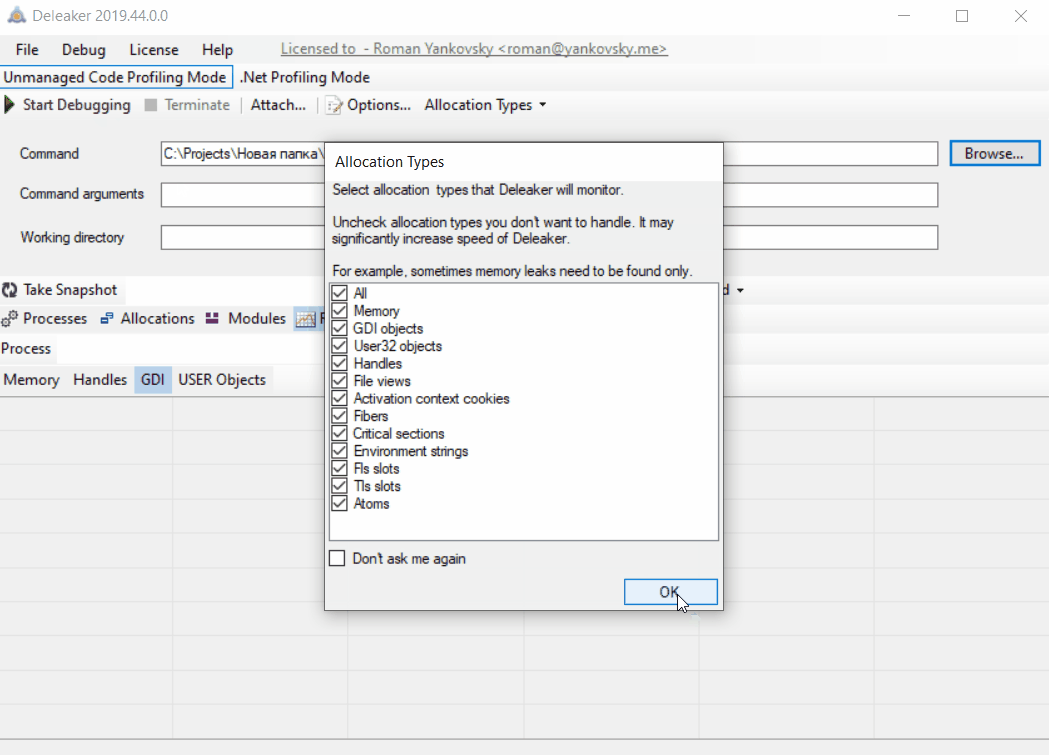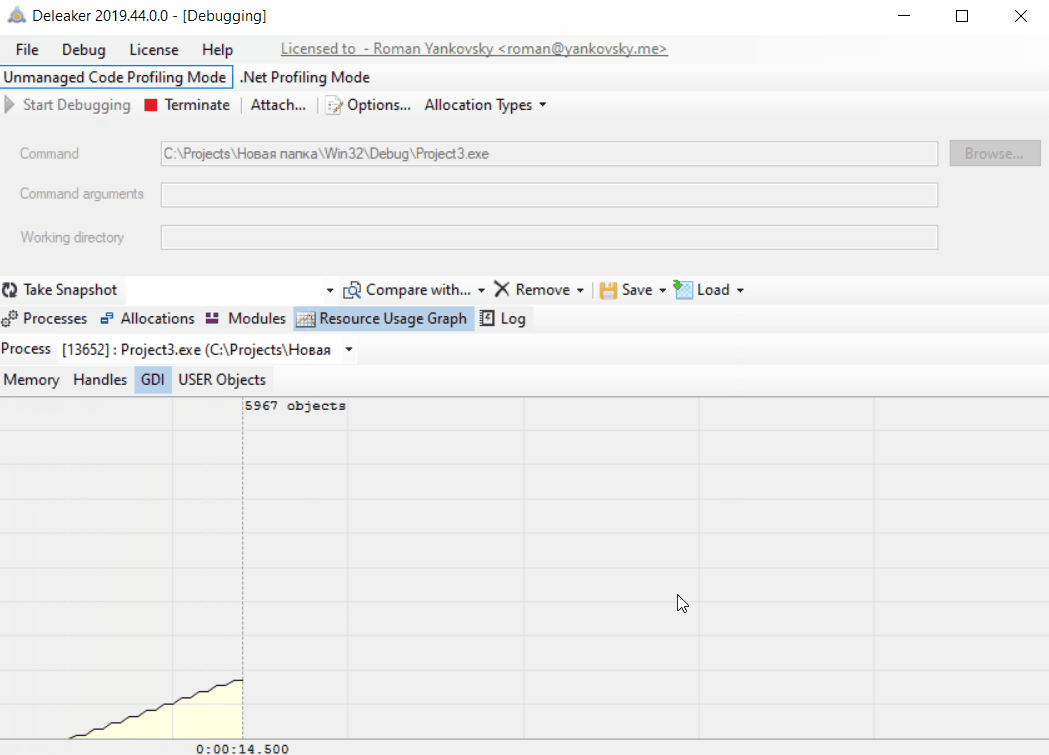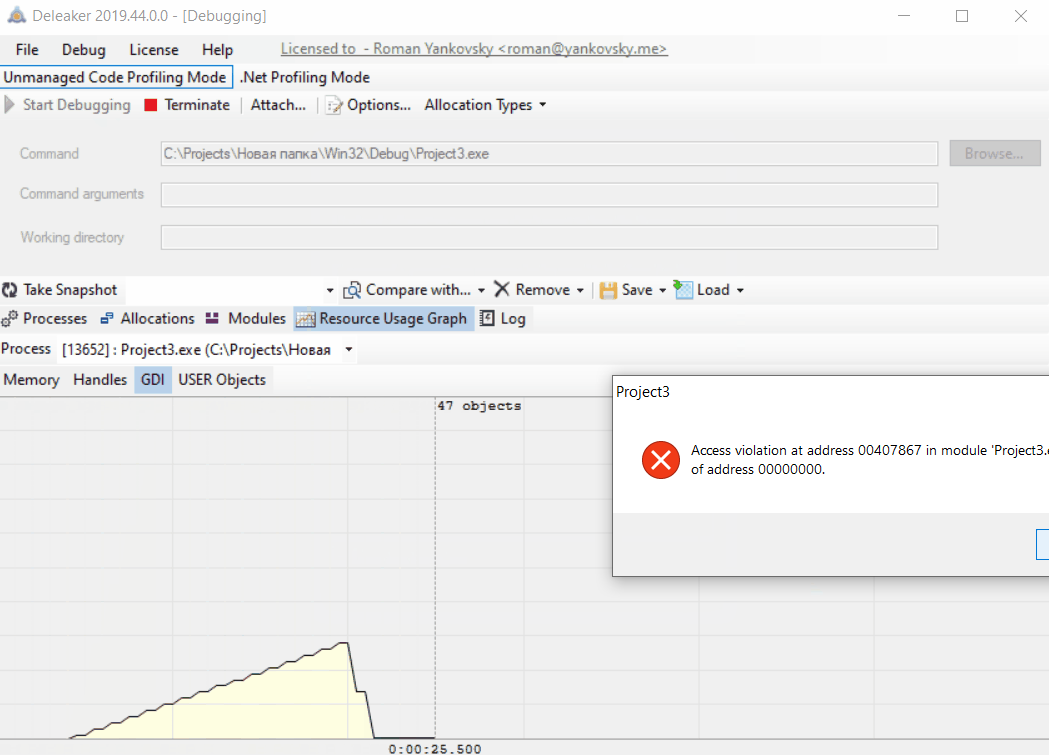
Here we can see that on peak there are more than 9000 GDI handles created. But 10000 is a default per-process limit for GDI handles.
But is it a leak, or we are just creating too many TPngImages? Let’s try to not create 5000 instances, but create an instance 5000 times and see. This way:
procedure TForm6.Button1Click(Sender: TObject);
var
Stream: TFileStream;
I: Integer;
Image: TPngImage;
begin
Stream := TFileStream.Create('C:\Program Files (x86)\Embarcadero\Studio\20.0\bin\iOSDelphiIcon.png', fmOpenRead);
try
// creating an instance of TPngImage 5000 times
for I := 1 to 5000 do
begin
Stream.Position := 0;
Image := LoadPngFromStream(Stream);
Image.Free;
end;
finally
Stream.Free;
end;
end;
Let’s see what happened.
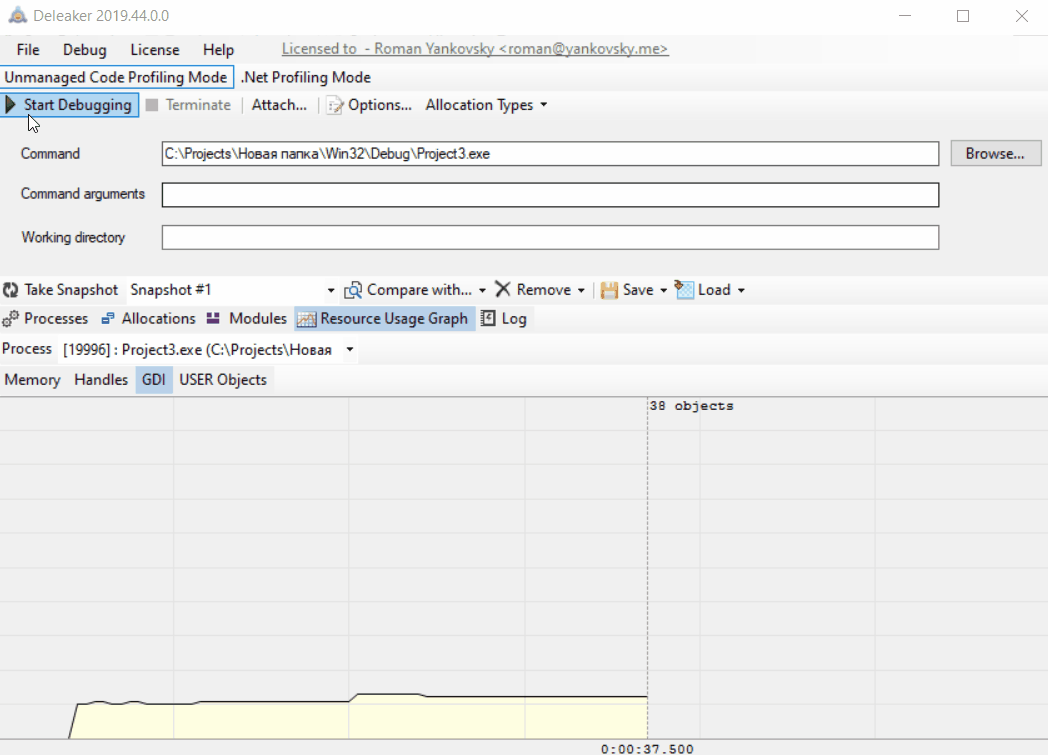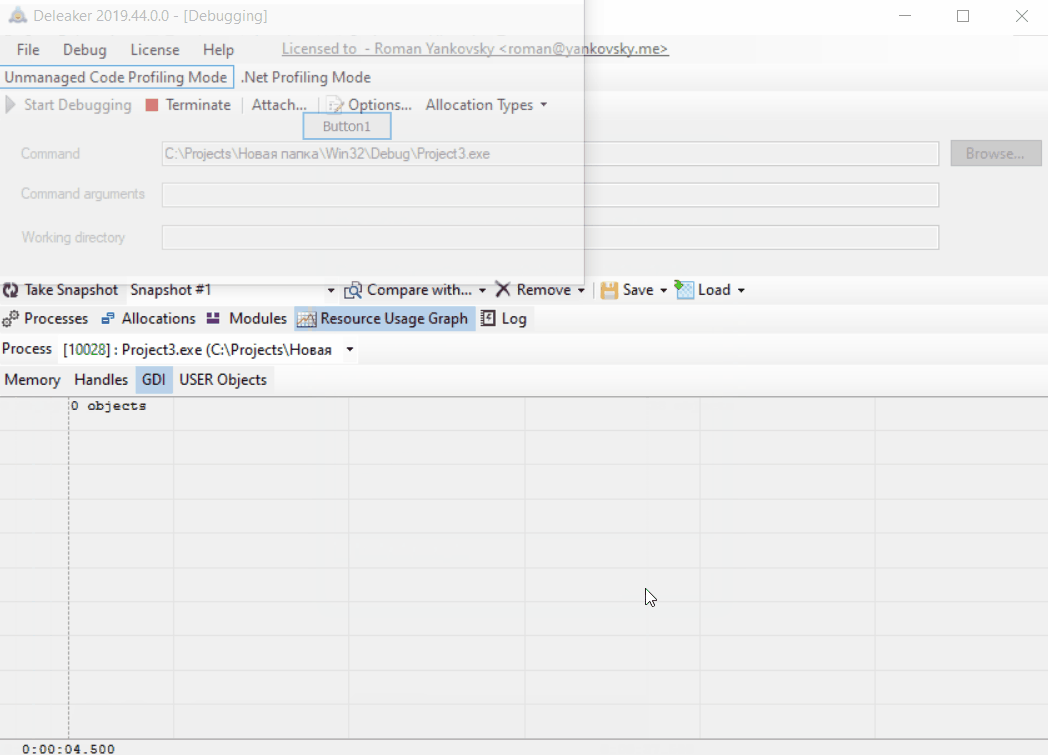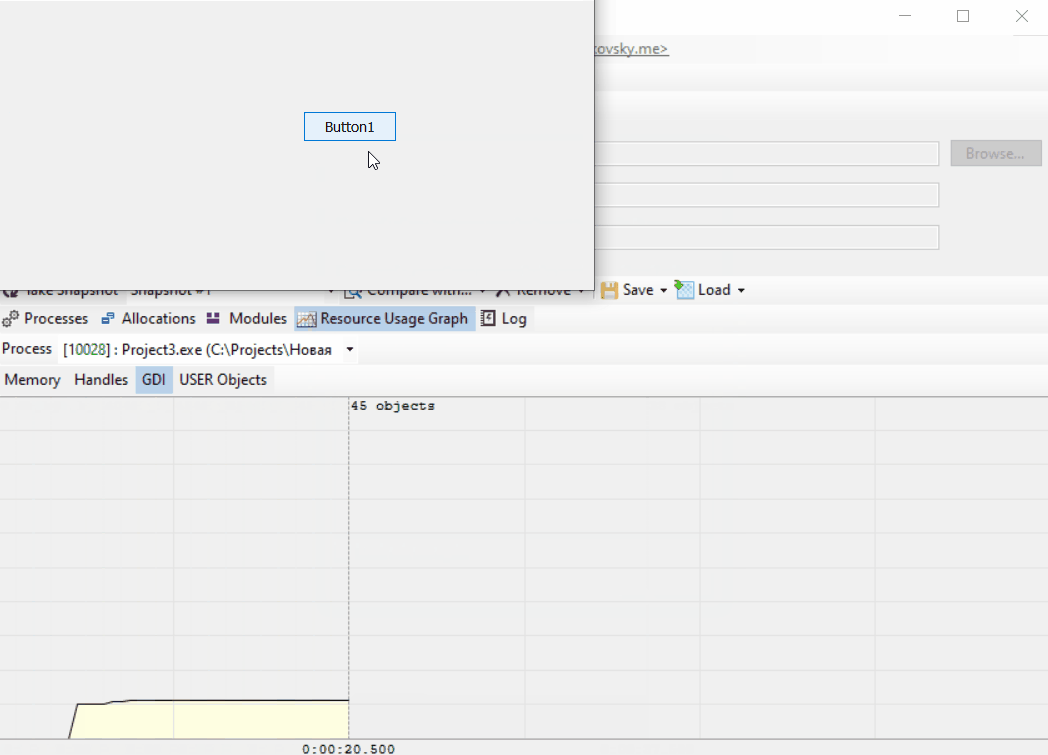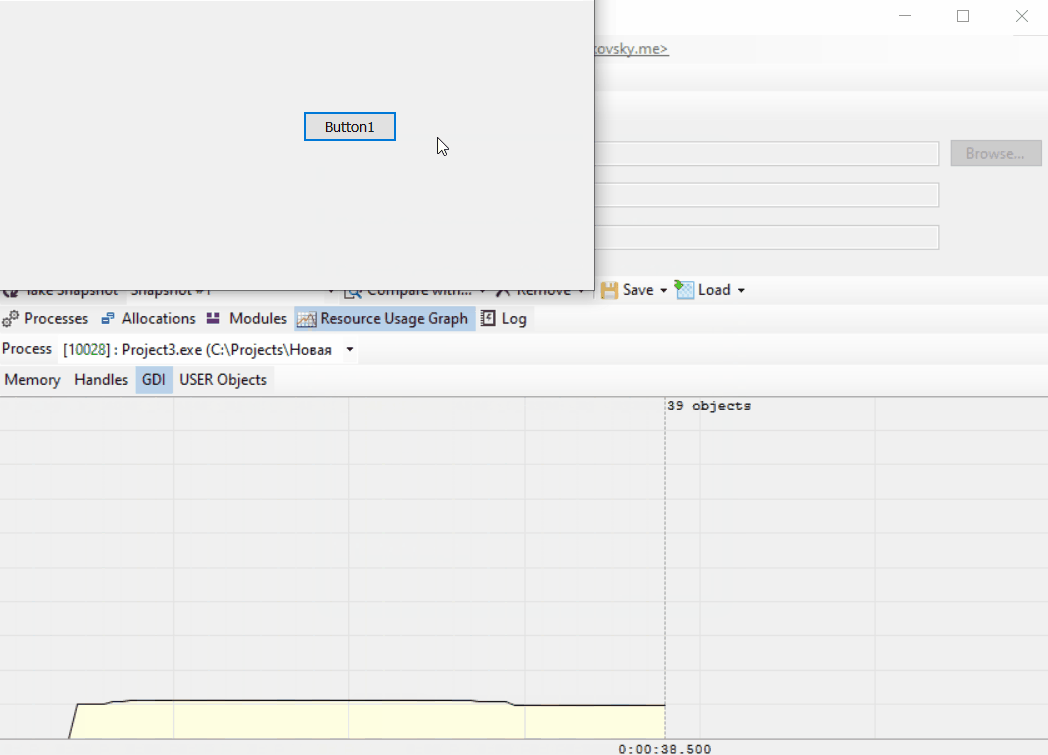
The chart is pretty stable. It doesn’t grow. It’s not a leak then. Just don’t create too many images :)
Graphics experts may give more insights. For instance, I’m not sure we need two GDI objects for each image and probably there is a room for optimization.
But so far let me show another Deleaker feature. Let’s write code that actually produce a memory leak. On line 9 I’ve changed True to False to not let ImageList release all TPngImage instances.
procedure TForm6.Button1Click(Sender: TObject);
var
Stream: TFileStream;
I: Integer;
ImageList: TObjectList<TPngImage>;
begin
Stream := TFileStream.Create('C:\Program Files (x86)\Embarcadero\Studio\20.0\bin\iOSDelphiIcon.png', fmOpenRead);
try
ImageList := TObjectList<TPngImage>.Create(False);
try
// creating 5000 instances of TPngImage
for I := 1 to 5000 do
begin
Stream.Position := 0;
ImageList.Add(LoadPngFromStream(Stream));
end;
finally
ImageList.Free;
end;
finally
Stream.Free;
end;
end;
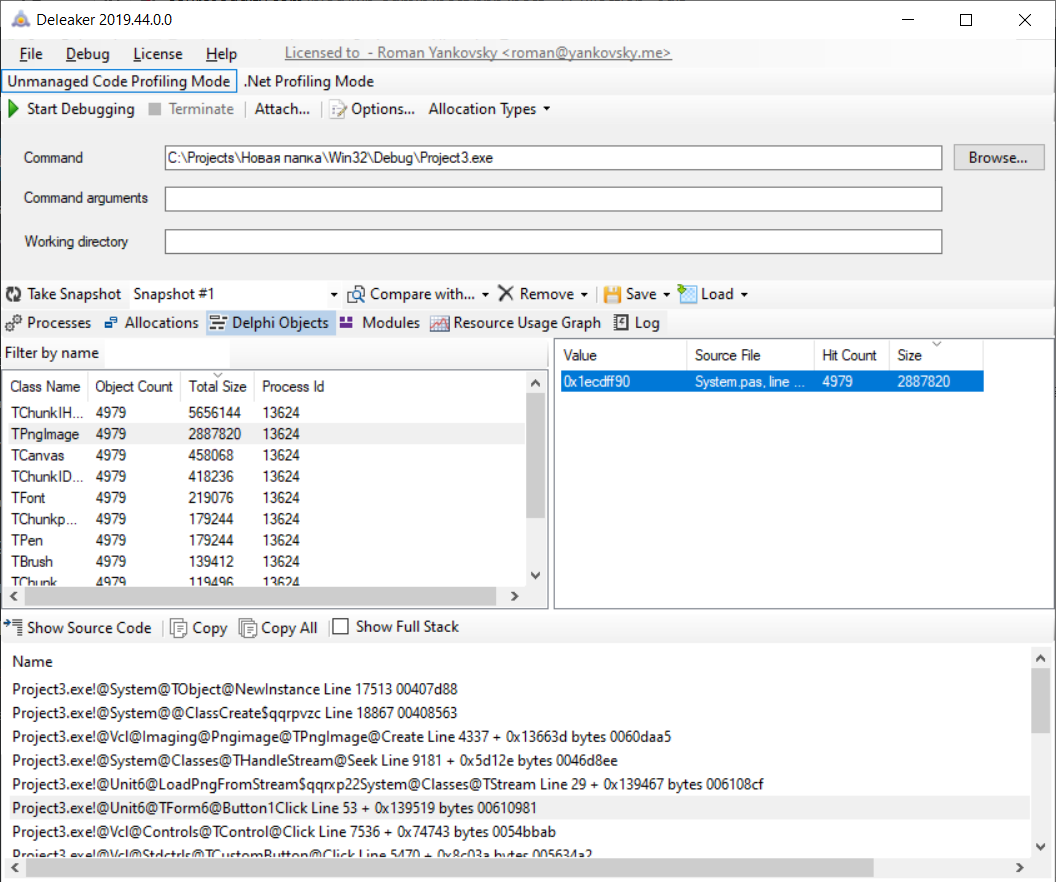
After running this under Deleaker I go to its Delphi Object tab and see a list of classes that were not released after I’ve exit the process. Hit Count tells how many of them were created, Total Size is their memory allocation. And the most important it shows stack trace below. So it’s easy to track down.
The leaks impact on end users often really painful, and it can be really hard to track down. So I think Deleaker is an useful tool.
